Marangoni magic: the art of forced fluid flow
- Mark Osborne
- Dec 19, 2023
- 4 min read
Updated: Feb 6, 2024

From the coffee ring left on the desk, the tears of wine clinging from your glass of good vintage, the swirling rainbows patterning a bubble surface, the foam topped beer [1-4]; you might ask, why the ring, the tears, the swirls, the head?
Mundane matters perhaps, but the Marangoni effect that gives rise to these phenomana plays an important role in many industrial processes, modern tenchnologies and life itself.
From the efficient drying of silicon wafers in the semiconductor industry, the high-res spotting of the humble inject printer, to nutrient transport in cells via cytoplasmic streaming and cell motility (e.g. cancer cell invasion) [5-7], the effect is a mesmerizing interplay between surface tension and fluid dynamics.
The effect is indeed pervasive, playing a crucial role in the spreading and stability of the sea surface microlayer, a biogenic skin that is critical to the climate through its role in regulating the water cycle [8].
Finally, as the phase down and out of oil becomes increasingly important in the drive to net zero, it is further found to impact key areas of the oil industry, from oil recovery to the dispersion of spills, and potentially the CO2 injection process associated with the nascent carbon capture and storage (CCS) industry [9,10].
Named after Italian physicist Carlo Marangoni [11], who was first to formulate the theory behind the phenomena, it is the flow of fluids down gradients in surface tension that creates those curious and captivating swirls on a bubble, ripples in a coffee stain, les larmes de vin.
The fluid flow is described by the beautiful maths behind the Navier-Stokes equations, derived from the works of Claude-Louis Navier [12] and George Stokes [13]. Here we show the elegance of the Stokeslet [14], a singularity in fluid mechanics that can be used to describe the motion of fluids under the action of a point force.
From a lost tweet in lockdown Nell demos Marangoni magic in #SciFriFun #lockdownlessons @CoolBrighton 10:58 AM · Jun 6, 2020
A classical demonstration is the "pepper and soap" experiment. Pour a water in bowl, shake pepper over the surface, add a single drop of washing-up liquid and, hey presto, the Marangoni magic sweeps the pepper to the edge of the bowl!
The soap acts to break the surface tension of the water and as it spreads from the centre a gradient builds between the low tension at the origin of the drop and high tension of water at the perimeter of the bowl.
Water flows out from the low tension centre and the pepper rides the wave to the edge until the soap and tension is even over the surface. In this case, the point force is radial and known as a Source with a velocity field that decays as the inverse of the square of the distance from the origin.
As the soap contacts the water, pepper streams from the centre, but slows rapidly toward the edge. The Stokeslet differs in that the force is unidirectional, acting in only one direction, along a single axis.
Microbubbles formed at nucleating heat spots in a liquid make a perfect paradigm for the Stokeslet, where a contrast in temperatures between hot vapour inside the bubble and cooler liquid outside creates a gradient in the surface tension across the bubble.
The gradient then drives fluid from regions of low tension to high and, as liquid flows to minimise the surface energy, viscous drag on the surrounding medium sets up the flow that characterises the Stokeslet.
We used plasmonics, the laser induced heating of metal nanoparticles, to generate bubbles in a viscous oil to study the Marangoni magic that happens when the Stokes flow is sandwiched between "non-slip" planes. In this case, glass slides sandwich the oil and nanoparticle filling on a microscope and a laser, focused on the oil, superheats the particles and nucleates bubble growth.

Movies then show the hypnotic, swirls of convective flow as the oil drags particles over the bubble surface down the temperature gradient (hot = low surface tension to cold = high).
As particles are lauched from the bubble surface, friction with oil close to the non-slip surfaces acts to slow the flow along the line of force, but increase speed normal to the point force by conservation of energy; and the particle turns aways from the bubble.
Under continuous heating, the flow keeps turning such that the energy flow forward is matched by reverse flows in the "wings of the butterfly" that characterises the convective flow of the Stokeslet observed around the bubble. Easy to describe in words, less easy by maths.
Solutions to the Navier-Stokes equations are non-trivial when constraints on the flow set by the glass slides, place the condition that there must be no flow at these "non-slip" planes; the flow velocity goes to zero at the glass.
With a little intuition we might imagine a "counter" image of the Stokeslet, reflected in the glass plane and flowing in the opposite direction, will cancel the flow at the boundary plane. Introduced by Sir William Thomson (Lord Klevin) in 1849 [15] to account for charge balancing in electrostatics, the "method of images" is widely used to solve boundary plane problems in physics.
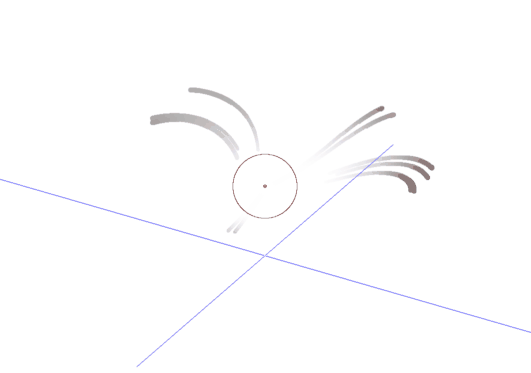
But intuition only goes so far, and an image of the Stokeslet alone does not complete the job.
Other neatly named singularities, the Potential Dipole and Stokes Doublet, must be added to the image to fully cancel flow at the glass.
If you like detail, checkout the script below that works up the Stokeslet maths and simulation algorithm. If not, then simply enjoy the movies. Combine with photocatalysis and the mesmerising magic of Marangoni hits another level!

PDF viewer may not work on mobile
Altering the coffee-ring effect by adding a surfactant-like viscous polymer solution.
Numerical modelling of the Marangoni effects induced by plankton-generated surfactants
Marangoni flow: An unknown mechanism for oil recovery during near-miscible CO2 injection.
Micro/nano-machines for spilled-oil cleanup and recovery: A review.
The self-propulsion of microscopic organisms through liquids.
* Links accesses Dec 2023


